Large Language Models Are Zero-Shot Problem Solvers — Just Like Modern Computers

Are large language models outlining a new kind of universal computing machines?

Language models (LMs) are trained specifically for one out of many natural language processing (NLP) tasks. By simply scaling them up to large LMs (LLMs), they emerge the ability to solve many other NLP tasks that they have not been trained for. This emergence of zero-shot problem solving ability of LLMs surprised the community. In this blog post, we draw an overlooked connection between LLMs and modern computers that also emerge zero-shot problem solving abilities. We discuss their similarities in capability, architecture, and history, and then use these similarities to motivate a different perspective on understanding LLMs and the prompting paradigm. We hope this connection can help us gain a deeper understanding of LLMs, and can spark discussions between the core computer science community and the foundation model community.

Introduction

Thanks to increasingly powerful computation infrastructures, we have witnessed many significant breakthroughs delivered by simply scaling up deep learning models in recent years. This is partially due to the empirical findings that for many tasks in natural language processing (NLP) and computer vision, the scale of a model and its test performance are so positively correlated that knowing either, one can even predict the other. Such relationship is described by the scaling laws. In other words, it is not surprising that a larger language model can achieve a better performance in the task of language modeling.

However, recent development in large language models (LLMs) such as GPT-3 and ChatGPT has attracted an unusual amount of interest from both the machine learning community as well as the general public. Apart from the imaginative conversations people had with LLMs, a more fundamental reason is that LLMs are not only showing improvements in language modeling but also showing the abilities to solve a wide range of NLP tasks including question answering, translation, summarization and even algorithmic tasks. This means by training on a single task, the model gains the ability to solve tasks it has never been trained for. Such an emergence of zero-shotWe use the term zero-shot to highlight that the model is not trained for the tested tasks (similar to its usage in the GPT-2 paper). This is sometimes also called universal or general problem solving. In many other LLM papers, zero-shot means no demonstration is provided during inference time in the prompt. Here we treat both zero-shot and few-shot prompting as examples of zero-shot problem solving. problem solving abilities in LLMs is surprising and was not predicted from the smaller scale models. It is still an open question how LLMs emerge with their abilities.

The phenomenon of a system showing spontaneous abilities that cannot be predicted when scaled up is known as emergence. Emergence is not a unique phenomenon that happens only in LLMs. It has been observed and discussed in many other subjects including physics and biology at least half a century ago. In the field of machine learning, emergence was also discussed and has inspired pioneer works such as the Hopfield network. The phenomenon is well explicated in an article by Philip W. Anderson with a concise title “More Is Different”.

Another example that has emergent ability are the computers we use in our daily life. The elementary components in modern computers are logic gates, which are designed to do simple Boolean operations only, e.g., AND, OR. But when we wire a large amount of them together, they emerge with the abilities to run various applications such as video games and text editors. If we phrase problems and tasks into programs, then computers can be seen as zero-shot problem solvers just like LLMs, since most of them are not designed or built for any specific program but as general purpose machines. Crucially, computer scientists have developed a host of tools to help understand and further exploit emergent capabilities, such as debuggers, or various high-level programming paradigms.

In this blog post, we connect the dots and draw an overlooked connection between these two zero-shot problem solvers, i.e., LLMs and computers. We believe their similarities outline the potential of using LLMs for a much more general problem solving setting, and their differences help us to understand the behaviors of LLMs and how to improve them. In particular, we illustrate how a good language model, which allows a concept to be encoded less ambiguously, is at the core of exploiting this new model of computation. We hope that this connection will spark new ideas for discussion such as computation theory, security, distributed computing etc. for LLMs.

A Tale of Two Zero-Shot Problem Solvers

In this section, we elaborate on the notion that large language models (LLMs) are zero-shot problem solvers in a similar way in which modern computers are zero-shot problem solvers, since they can both solve much more general problems than those they have been trained or hardcoded for. However, we understand much better how such ability emerged in computers than LLMs. Here, we look into the similarities as well as the differences in the formulations and the histories of both models of computation, and try to understand how LLMs emerged with their abilities.

Modern Computers Computers have undergone several transitions from specialized to universal machines (see Figure 1(c)). As we will discuss below, this transition is similar to the recent history of LLMs. Alan Turing had an early vision of a universal computing machine that was way ahead of its time because the real machines around the time were only constructed for special tasks, such as breaking encrypted communication during wartime. To follow Turing’s vision and to avoid building a different machine from scratch for a new task, early computer scientists, built machines with a large collection of different arithmetic units and switches (e.g., ENIAC). By wiring up these units differently (i.e., programming) and piping the input data through, the machine was able to solve different tasks. While this made it possible to ‘‘reprogram’’ (i.e., rewire) the computer, the program was still part of the hardware wiring, and any changes to it had to be done manually. The later invention of stored-program computers overcame this limitation and led to even more universal computing machines. Here, the central idea, expressed in the von Neumann architecture, was to represent programs as data rather than as wiring setups. This allowed computers to read and solve arbitrary programs for which they were not set up by wiring. In other words, they become zero-shot problem solvers.

Large Language Models Written language can be formed by sequences of tokens. A language model learns mappings to the next token \(t_i\) from its prefix. Such a mapping can be represented as a conditional probability distribution (see Figure 1(b)). The joint probability of the sequence \(p(\boldsymbol{t})\) is the product of the conditional probabilities, i.e., \begin{equation} p(\boldsymbol{t}) = p(t_1)\prod_{i=2}^{N} p(t_i | t_1, \dots, t_{i-1}). \end{equation} A popular method to model these conditional probabilities is to use Transformers and train under self-supervision. With increasing scale of these language models, they turn out to emerge the ability to solve tasks other than language modeling (i.e., they are zero-shot problem solvers), and we call them large language models for distinction.

Connecting the Dots

Here, we compare the architectures and survey the histories of computers and LLMs, which turned out to be surprisingly similar (see Figure 1). Their likeness might not be a coincidence, and can provide clues for us to understand how LLMs emerge with their abilities.

Similar frameworks Both computers and LLMs can be seen as mappings from \(\mathcal{P}\) to \(\mathcal{A}\) (Figure 1(a)). Given a program \(\mathcal{P}\), a computer will execute \(\mathcal{P}\) and return the answer \(\mathcal{A}\) when the program terminates. This mapping is deterministic, which means if \(\mathcal{P}\) is a correct implementation of a suitable algorithm, then \(\mathcal{A}\) is the correct answer to the problem. Similarly, given a prompt \(\mathcal{P}\), an LLM will infer and return an answer \(\mathcal{A}\). However, this mapping is stochastic and follows the conditional distribution \(p(\mathcal{A} | \mathcal{P})\) captured by the LLM. In addition, the interactive feature of LLMs allows us to easily include previous prompts and answers into the new prompt, i.e., \(\mathcal{P}_i = [\mathcal{P}_{i-1}, \mathcal{A}_{i-1}, new]\).

Similar level of abstractions Both computers and LLMs consist of a problem translator on top of a foundational compute architecture (Figure 1(b)). The problem translator turns problems written in a human readable language into some native representation of the compute architecture (bit strings for computers, vectors for LLMs). The compute architecture is formed by a large collection of simple components (logic gates for computers, matrix multiplications and activation functions for LLMs). In both computers and LLMs, the respective compute architecture is able to do arbitrary computations due to both the scale (i.e., the quantity) and the universality of the involved components.

Similar histories Both computers and LLMs had a similar path of evolution from task-specific to general-purpose problem solvers (Figure 1(c)). Early approaches to NLP designed and trained a model specifically for a given task, e.g., question answering (QA). To create more general solutions, people then experimented with model architectures that were trained on a fixed set of tasks, specified by a task identification tag. Similar to the von Neumann architecture of computers, the next important development was to represent the task description in the same format as the input and output, i.e., describing a task in natural language rather than using a special tag. This resulted in a training objective very similar to language modeling. Inspired by this, Radford et al. trained a pure (but very large) language model (i.e., GPT-2) and showed its ability to solve a range of different NLP tasks beyond language modeling.

Fundamental Difference

Computers and LLMs as zero-shot problem solvers are similar in many ways, but there is one major distinction determined that one cannot be replaced by the other. LLMs are more accessible for the general public since LLMs understand natural language, but at the same time, natural language is ambiguous and difficult to describe a problem precisely. Therefore, LLMs might misunderstand what we ask and not able to solve the problem we really want to solve. In contrast, computers are excellent problem solvers because programming languages are formal language, and we can precisely describe a problem to computers without ambiguity. However, what we traded off is the accessibility, since users for computers are required to learn these formal languages in order to gain full access to computer’s problem solving ability, which is not the case for LLMs.

Lessons to Learn

The connections between computers and LLMs identified above reveal two important findings about zero-shot problem solvers. Here, we identify two essential building blocks for them, and we point out a direction to improve LLMs which explains the current focus in the community.

Finding 1

The zero-shot problem solving ability only emerges when we combine a powerful compute architecture with a suitable problem translator.

Computational ability is not as rare a property as we might think. There are many, even simple physical systems that can compute, but zero-shot problem solving requires an additional layer of abstraction on top of computation that translates new problems into the type of computations that the system can perform. For example, many problems can be phrased as minimization problems, i.e., finding the lowest point on some surface. A simple compute architecture capable of solving such an optimization problem could drop a ball onto a physical manifestation of a given surface and record where the ball eventually stops. While, in principle, many problems can be phrased as such minimization problems, in practice, the problems humans want to solve are typically described in a more readable form. Without an additional unit that translates the human-readable description into a surface whose lowest point we want to find, the above computation architecture is not capable of zero-shot problem solving.

Both computers and LLMs have very powerful compute architectures, which can be shown to be Turing complete. What turns computers and LLMs into zero-shot problem solvers is the fact that they also have powerful problem translators, which map between the native language of the compute architecture and a high-level language, preserving the computation power.

Finding 2

Minimizing the gap between the language model of LLMs and the internal language model of a user is at the core of unlocking the full problem solving ability of LLMs.

As we have argued above, ensuring that a solver understands the problem or instruction is key for solving it. Computers have been excellent problem solvers for the past decades because formal languages are designed to be precise. This means given a piece of code in some formal language, there is only one correct interpretation (illustrated as a delta distribution in Figure 2 bottom left) and good programmers are expected to understand the language fairly well (see sharp peak in Figure 2 top left). In other words, the models that humans and computers have of a formal language are both relatively precise, and the two are closely aligned with each other. In contrast, natural language is inherently imprecise as there are often many correct interpretations given a sentence. Moreover, both humans and LLMs learn natural language from data rather than from a specification, so their two models will typically be somewhat misaligned from each other.

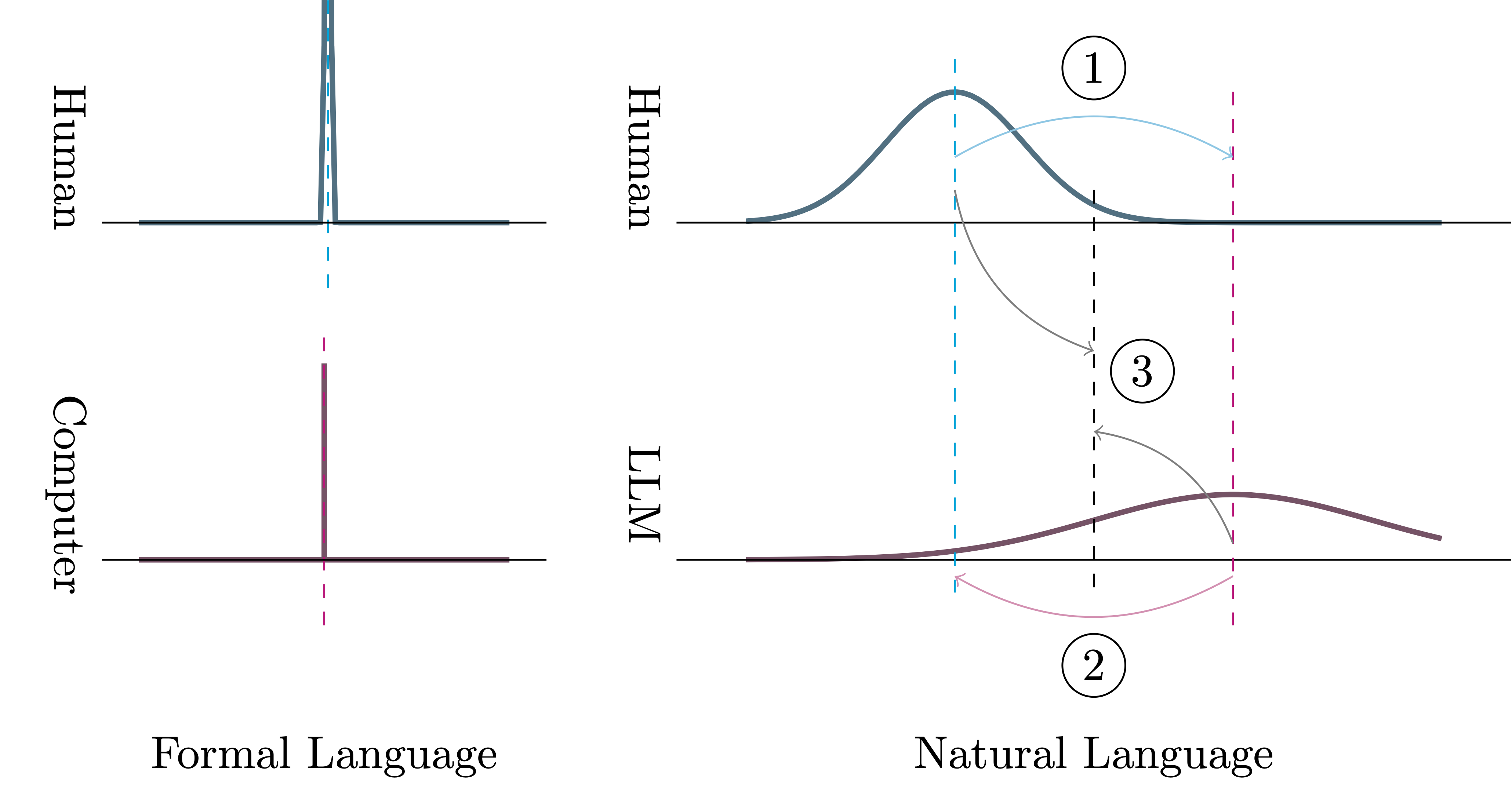
Figure 2: Communication gaps between human and the solver with different languages. Language ambiguity is depicted by variance, model misalignment is depicted by the two separate means.

Many of the existing works on LLMs as zero-shot problem solvers can be understood as a spectrum of methods for minimizing the communication gap between humans and LLMs. At one end of the spectrum, we humans can adapt our internal language models towards the language models of LLMs (① in Figure 2), e.g., by incorporating certain signalling phrases into our prompts that empirically improve the quality of answers, such as “Let’s think step by step”. At the other end of the spectrum, we can adapt LLMs towards our internal language models (② in Figure 2). This can be done during training (e.g., as in InstructGPT and ChatGPT, which were trained with human feedback), or after training (e.g., personalizing the model by few-shot prompting, i.e., prefixing prompts with examples of similar problems and their solutions or with a conversation history). Most prompting research falls somewhere in between these two extremes, where humans and LLMs adapt their models towards each other (③ in Figure 2).